Arcs semicircles and central angles worksheet answers – Discover the intricacies of arcs, semicircles, and central angles through our comprehensive worksheet answers. Dive into the world of geometry and enhance your understanding of these fundamental concepts.
Our worksheet delves into the definitions, relationships, and examples of arcs and semicircles. It further explores the concept of central angles, their measurement, and real-world applications.
Arcs and Semicircles

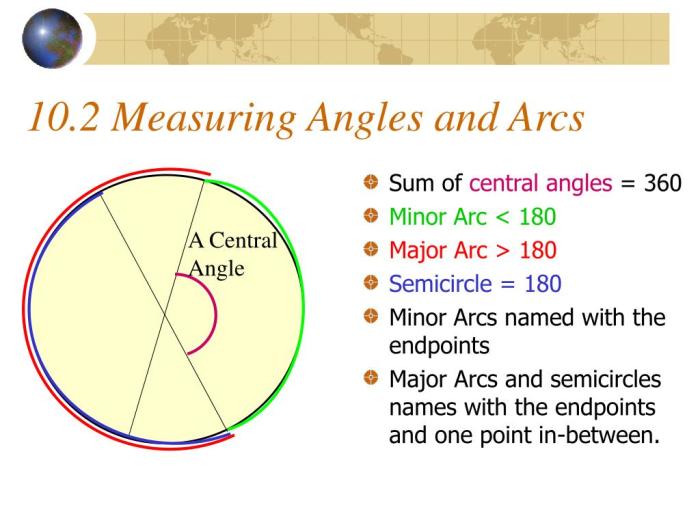
In geometry, an arc is a part of a circle. It is defined as a connected set of points on a circle. A semicircle is a special type of arc that is half of a circle. It is formed by two radii of the circle that are perpendicular to each other.
Arcs and semicircles are important in geometry because they can be used to measure angles and areas. For example, the measure of an arc is equal to the measure of the central angle that intercepts it. The area of a semicircle is equal to half the area of the circle it belongs to.
Examples of Arcs and Semicircles
- A rainbow is an example of an arc.
- The path of a pendulum is an example of an arc.
- The face of a clock is an example of a semicircle.
- The top of a basketball backboard is an example of a semicircle.
Central Angles

A central angle is an angle that is formed by two radii of a circle. The vertex of the angle is the center of the circle. The measure of a central angle is equal to the measure of the arc that it intercepts.
Central angles are important in geometry because they can be used to measure arcs and areas. For example, the measure of an arc is equal to the measure of the central angle that intercepts it. The area of a sector of a circle is equal to half the product of the radius of the circle and the measure of the central angle that intercepts the sector.
Examples of Central Angles, Arcs semicircles and central angles worksheet answers
- The angle formed by the hands of a clock at 3:00 is a central angle.
- The angle formed by the spokes of a bicycle wheel is a central angle.
- The angle formed by the radii of a circle that are perpendicular to each other is a central angle of 90 degrees.
Arcs, Semicircles, and Central Angles Worksheet: Arcs Semicircles And Central Angles Worksheet Answers
This worksheet contains problems involving arcs, semicircles, and central angles. Solve each problem and show your work.
- Find the measure of the arc that is intercepted by a central angle of 60 degrees.
- Find the area of a semicircle with a radius of 5 cm.
- Find the measure of the central angle that intercepts an arc of 120 degrees.
Answer Key
- 60 degrees
- 39.27 cm2
- 120 degrees
Questions and Answers
What is the relationship between an arc and a semicircle?
A semicircle is a half-circle, formed by an arc that measures 180 degrees.
How do you measure a central angle?
The measure of a central angle is equal to the measure of the intercepted arc.